The code below gives a simple implementation of the Metropolis and Metropolis-in-Gibbs sampling algorithms, which are useful for sampling probability densities for which the normalizing constant is difficult to calculate, are irregular, or have high dimension (Metropolis-in-Gibbs).

## Metropolis sampling
## x    - current value of Markov chain (numeric vector)
## targ - target log density function
## prop - function with prototype function(x, ...) that generates 
##   a proposal value from a symmetric proposal distribution
library('mvtnorm')
prop_mvnorm <- function(x, ...)
  drop(rmvnorm(1, mean=x, ...))
metropolis <- function(x, targ, prop=prop_mvnorm, ...) {
  xnew <- prop(x)
  lrat <- targ(xnew, ...) - targ(x, ...)
  if(log(runif(1)) < lrat)
    x <- xnew
  return(x)
}

## Metropolis-in-Gibbs sampling
## x    - current value of Markov chain (numeric vector)
## targ - target log density function
## ...  - arguments passed to 'targ'
gibbs <- function(x, targ, ...) {
  for(i in 1:length(x)) {
    ## define full conditional
    targ1 <- function(x1, ...) {
      x[i] <- x1
      targ(x, ...)
    }
    ## sample using Metropolis algorithm
    x[i] <- metropolis(x[i], targ1, ...)
  }
  return(x)
}

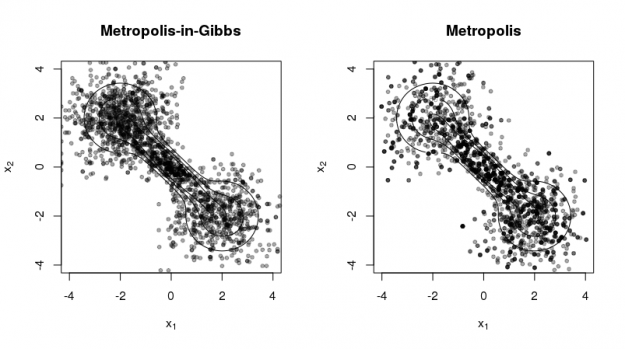
The following code produces the figure below to illustrate the two methods using a 'dumbell' distribution (cf. R package 'ks' vignette).

### The code below illustrates the use of the functions above 

## target 'dumbell' density (c.f., R package 'ks' vignette)
library('ks')
mus <- rbind(c(-2,2), c(0,0), c(2,-2))
sigmas <- rbind(diag(2), matrix(c(0.8, -0.72, -0.72, 0.8), nrow=2), diag(2)) 
cwt <- 3/11
props <- c((1-cwt)/2, cwt, (1-cwt)/2)
targ_test <- function(x, ...)
  log(dmvnorm.mixt(x, mus=mus, Sigmas=sigmas, props=props))

## plot contours of target 'dumbell' density
set.seed(42)
par(mfrow=c(1,2))
plotmixt(mus=mus, Sigmas=sigmas, props=props,
         xlim=c(-4,4), ylim=c(-4,4),
         xlab=expression(x[1]),
         ylab=expression(x[2]),
         main="Metropolis-in-Gibbs")

## initialize and sample using Metropolis-in-Gibbs
xcur <- gibbs(c(0,0), targ_test, sigma=vcov_test)
for(j in 1:2000) {
  xcur <- gibbs(xcur, targ_test, sigma=vcov_test)
  points(xcur[1], xcur[2], pch=20, col='#00000055')
}

## plot contours of target 'dumbell' density
plotmixt(mus=mus, Sigmas=sigmas, props=props,
         xlim=c(-4,4), ylim=c(-4,4),
         xlab=expression(x[1]),
         ylab=expression(x[2]),
         main="Metropolis")

## initialize and sample using Metropolis
xcur <- metropolis(c(0,0), targ_test, sigma=vcov_test)
for(j in 1:2000) {
  xcur <- metropolis(xcur, targ_test, sigma=vcov_test)
  points(xcur[1], xcur[2], pch=20, col='#00000055')
}

The figure illustrates two contrasting properties of the two methods:

1. Metropolis-in-Gibbs samples can get 'stuck' in certain regions of the support, especially when there are multiple modes and/or significant correlation among the random variables. This is not as much a problem for Metropolis sampling.
2. Metropolis sampling can produce fewer unique samples due to the poor approximation of the proposal density to the target density. This occurs more often for high-dimensional target densities.