In writing this post, I discovered that this question is very common1,2,3,4, and that my treatment will be relatively simplistic (I almost didn't post it, but this blog has been dark for a while...). There are many issues to consider beyond total worth, including the liquidity of savings versus home equity, tax and tax-sheltered savings, variability in interest rates, etc.
Consider the problem where a certain amount of monthly income 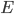 is available to either invest in savings (i.e., savings or money market account, CD, mutual funds, stocks, other unwieldy financial instruments5), or to make an additional payment towards a home mortgage. The relevant quantities are denoted
is available to either invest in savings (i.e., savings or money market account, CD, mutual funds, stocks, other unwieldy financial instruments5), or to make an additional payment towards a home mortgage. The relevant quantities are denoted
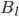 ,
, 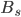 - Loan or Savings Balance
- Loan or Savings Balance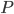 - Initial Loan (Principal)
- Initial Loan (Principal)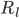 ,
, 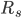 - Monthly Interest Rates
- Monthly Interest Rates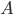 - Minimum Monthly Mortgage Payment
- Minimum Monthly Mortgage Payment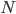 - Number of Payments / Investments
- Number of Payments / Investments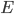 - Unallocated Earnings
- Unallocated Earnings
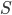 - Monthly Savings (
- Monthly Savings (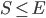 )
)
Hence, 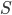 is the portion of
is the portion of 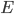 that is invested, where the remainder of
that is invested, where the remainder of 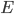 is used to reduce the mortgage balance. Our problem is to select
is used to reduce the mortgage balance. Our problem is to select 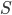 .
.
The balance formulae for savings and loans are, respectively,
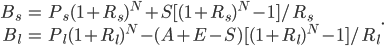
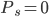 ). In this scenario, the total accumulated value is the sum of home equity and savings
). In this scenario, the total accumulated value is the sum of home equity and savings 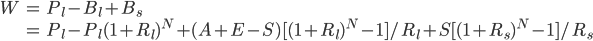
By factoring
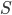 , we find that
, we find that 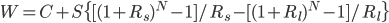 , where
, where 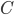 is constant with respect to
is constant with respect to 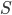 . Hence, it's optimal to save all of
. Hence, it's optimal to save all of 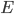 (i.e.,
(i.e.,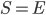 ) when
) when 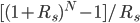 is greater than
is greater than 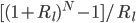 , but to save none of
, but to save none of 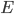 (i.e., to apply
(i.e., to apply 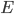 towards mortgage principle) when the opposite is true. What's interesting here, and not immediately intuitive, is that optimality depends only on the related interest rates, but not the mortgage balance!
towards mortgage principle) when the opposite is true. What's interesting here, and not immediately intuitive, is that optimality depends only on the related interest rates, but not the mortgage balance!