In writing this post, I discovered that this question is very common^1,2,3,4, and that my treatment will be relatively simplistic (I almost didn't post it, but this blog has been dark for a while...). There are many issues to consider beyond total worth, including the liquidity of savings versus home equity, tax and tax-sheltered savings, variability in interest rates, etc.

Consider the problem where a certain amount of monthly income 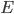$E$ is available to either invest in savings (i.e., savings or money market account, CD, mutual funds, stocks, other unwieldy financial instruments⁵), or to make an additional payment towards a home mortgage. The relevant quantities are denoted

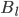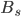• $B_l$, $B_s$ - Loan or Savings Balance
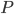• $P$ - Initial Loan (Principal)
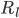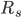• $R_l$, $R_s$ - Monthly Interest Rates
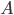• $A$ - Minimum Monthly Mortgage Payment
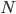• $N$ - Number of Payments / Investments
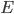• $E$ - Unallocated Earnings
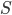• $S$ - Monthly Savings ($S \leq E$)

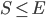Hence, 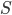$S$ is the portion of 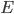$E$ that is invested, where the remainder of 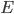$E$ is used to reduce the mortgage balance. Our problem is to select $S$.

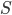The balance formulae for savings and loans are, respectively,

$$\begin{array}{r c l}B_s & = & P_s(1+R_s)^N + S[(1+R_s)^N - 1]/R_s \\ B_l & = & P_l(1+R_l)^N - (A + E - S)[(1+R_l)^N - 1]/R_l\end{array}.$$

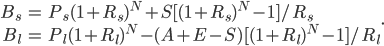
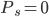Derivation of these formulae⁶ relies on the sum of geometric series⁷. For simplicity, we assume that no savings have been accumulated thus far (i.e., $P_s = 0$). In this scenario, the total accumulated value is the sum of home equity and savings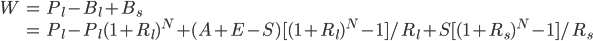

$$\begin{array}{r c l}W & = & P_l - B_l + B_s \\ & = & P_l - P_l(1+R_l)^N + (A + E - S)[(1+R_l)^N - 1]/R_l + S[(1+R_s)^N - 1]/R_s \end{array}$$

By factoring 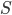$S$, we find that 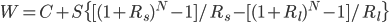$W = C + S\{[(1+R_s)^N-1]/R_s - [(1+R_l)^N-1]/R_l\}$, where 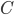$C$ is constant with respect to 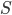$S$. Hence, it's optimal to save all of 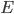$E$ (i.e.,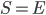$S=E$) when 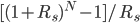$[(1+R_s)^N-1]/R_s$ is greater than 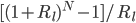$[(1+R_l)^N-1]/R_l$, but to save none of 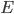$E$ (i.e., to apply 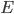$E$ towards mortgage principle) when the opposite is true. What's interesting here, and not immediately intuitive, is that optimality depends only on the related interest rates, but not the mortgage balance!