I recently posted the message below with regard to sampling from the truncated exponential distribution. I left out the derivation of the CDF (mostly because text math is ugly), so I've included it here. There is also a short JSS article about truncated distributions in R. This problem in particular may likely be found in an introductory text on survival analysis or probability theory.
Where 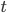 is the level of truncation and
is the level of truncation and 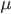 is the rate, the normalization constant
is the rate, the normalization constant 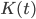 is given by
is given by
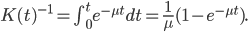
The truncated exponential CDF is then
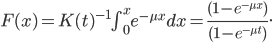
Solving for the inverse CDF yields the itexp function below. From the R-help list:
Since there is a simple closed form for the truncated exponential CDF, you can use inverse transform sampling. I believe this is quite common in survival analysis methods. The first step is to compute and write an R function to compute the inverse CDF for the truncated exponential, say
itexp <- function(u, m, t) { -log(1-u*(1-exp(-t*m)))/m }where u is the quantile, m is the rate, and t is the level of truncation. Next, we draw from the truncated exponential with something like
rtexp <- function(n, m, t) { itexp(runif(n), m, t) }