JW Emerson, WA Green, B Schloerke, J Crowley, D Cook, H Hofmann, H Wickham (2013) The Generalized Pairs Plot. Journal of Computational and Graphical Statistics 22(1). Here's a free preprint version.
Until this new paper and implementation by Emerson et al., there were no widely available pairs plots that accommodated both numerical and categorical fields. ***Update 3/29/2013: ggpairs in the GGally package has been around since 2010***. A browse through the R Graph Gallery confirms this (as of 1/30/2013). See here too: a post on the Quick-R blog. I had been working on such a plot when I discovered the above article. Hence, I'm using this post to share my work, which I will probably abandon in favor of the above.
Any number of statistical graphics might be used instead of a scatterplot for numeric/numeric pairs; maybe a hexbin plot. A sieve plot or an association plot might be used as an alternative to the mosaicplot for factor/factor pairs. A beeswarm boxplot plot might be used in place of side-by-side boxplots for numeric/factor pairs.
Here was my provisional version of the generalized pairs plot, which I had called an 'association matrix plot':
pairsdf <- function(df, abbr = TRUE, abbr.len = 4) {
par(mfrow = rep(length(df), 2))
for (row in 1:length(df)) {
xr <- df[[row]]
if (is.character(xr) || is.logical(xr))
xr <- as.factor(xr)
if (is.factor(xr) && abbr)
levels(xr) <- abbreviate(levels(xr), 4)
for (col in 1:length(df)) {
xc <- df[[col]]
if (is.character(xc) || is.logical(xc))
xc <- as.factor(xc)
if (inherits(xc, "factor") && abbr)
levels(xc) <- abbreviate(levels(xc), 4)
cnm <- names(df)[col]
rnm <- names(df)[row]
if (col == row) {
plot(c(0, 1), c(0, 1), type = "n", xaxt = "n",
yaxt = "n", bty = "n", xlab = "", ylab = "",
main = "")
text(x = 0.5, y = 0.5, labels = cnm, adj = c(0.5,
0.5), cex = 2)
}
else {
iscf <- is.factor(xc)
iscn <- is.numeric(xc)
isrf <- is.factor(xr)
isrn <- is.numeric(xr)
if (isrf && iscf) {
mosaicplot(table(xc, xr), xlab = cnm, ylab = rnm,
main = "", las = 2, color = TRUE, cex = 1.1)
}
else if (isrn && iscn) {
plot(xc, xr, xlab = cnm, ylab = rnm, main = "",
las = 2, cex = 1.1)
}
else if (isrn && iscf) {
boxplot(xr ~ xc, xlab = cnm, ylab = rnm, main = "",
las = 2, cex = 1.1)
}
else if (isrf && iscn) {
boxplot(xc ~ factor(xr, levels = rev(levels(xr))),
xlab = cnm, ylab = rnm, main = "", las = 2,
cex = 1.1, horizontal = TRUE)
}
else stop("urecognized variable type")
}
}
}
}
Below are several association matrix plots generated by the above function (i.e., pairsdf) for data sets found in the MASS package. When there are many fields, I recommend using three to four square inches per plot.
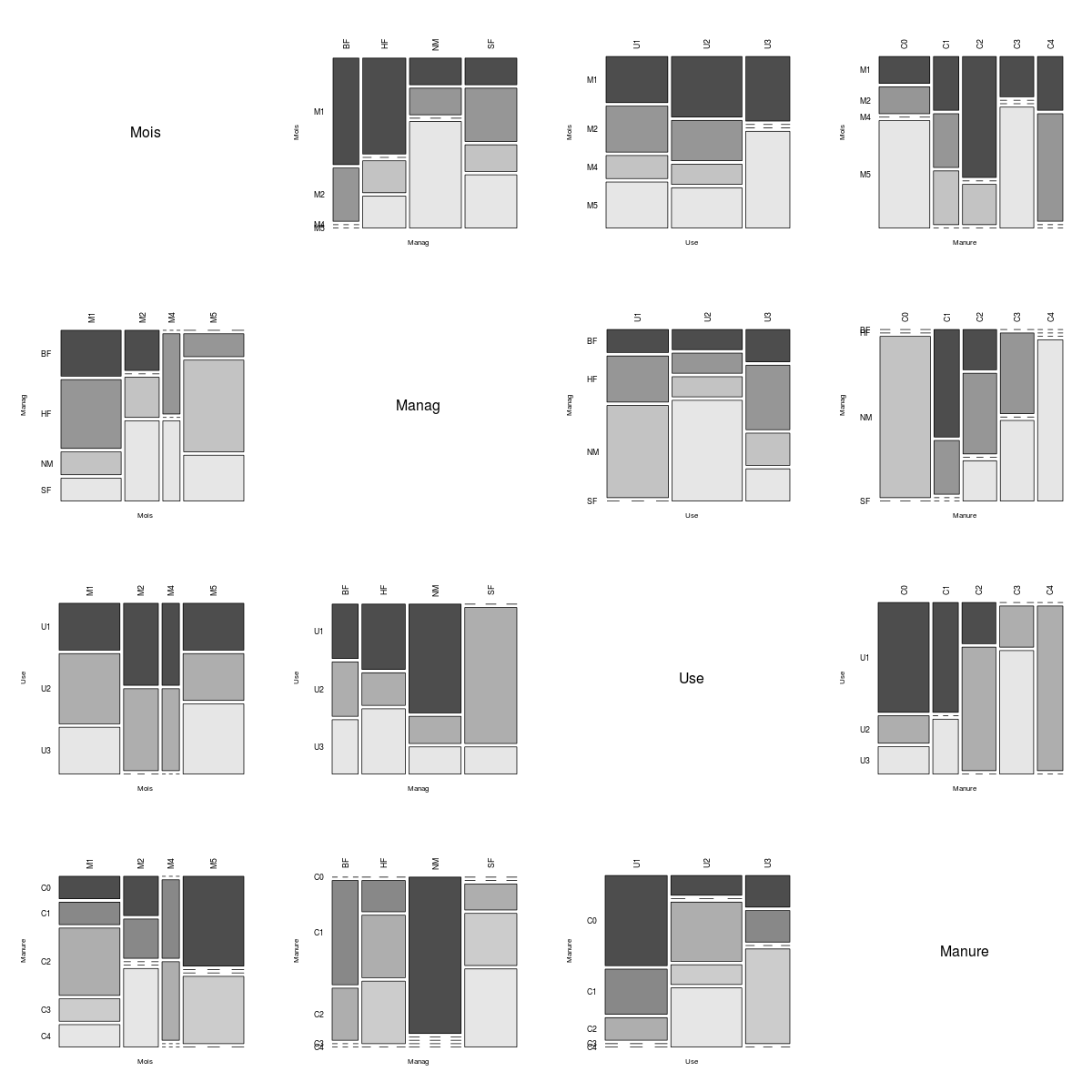
It's easy to see that the coop data set describes a simple factorial experiment.
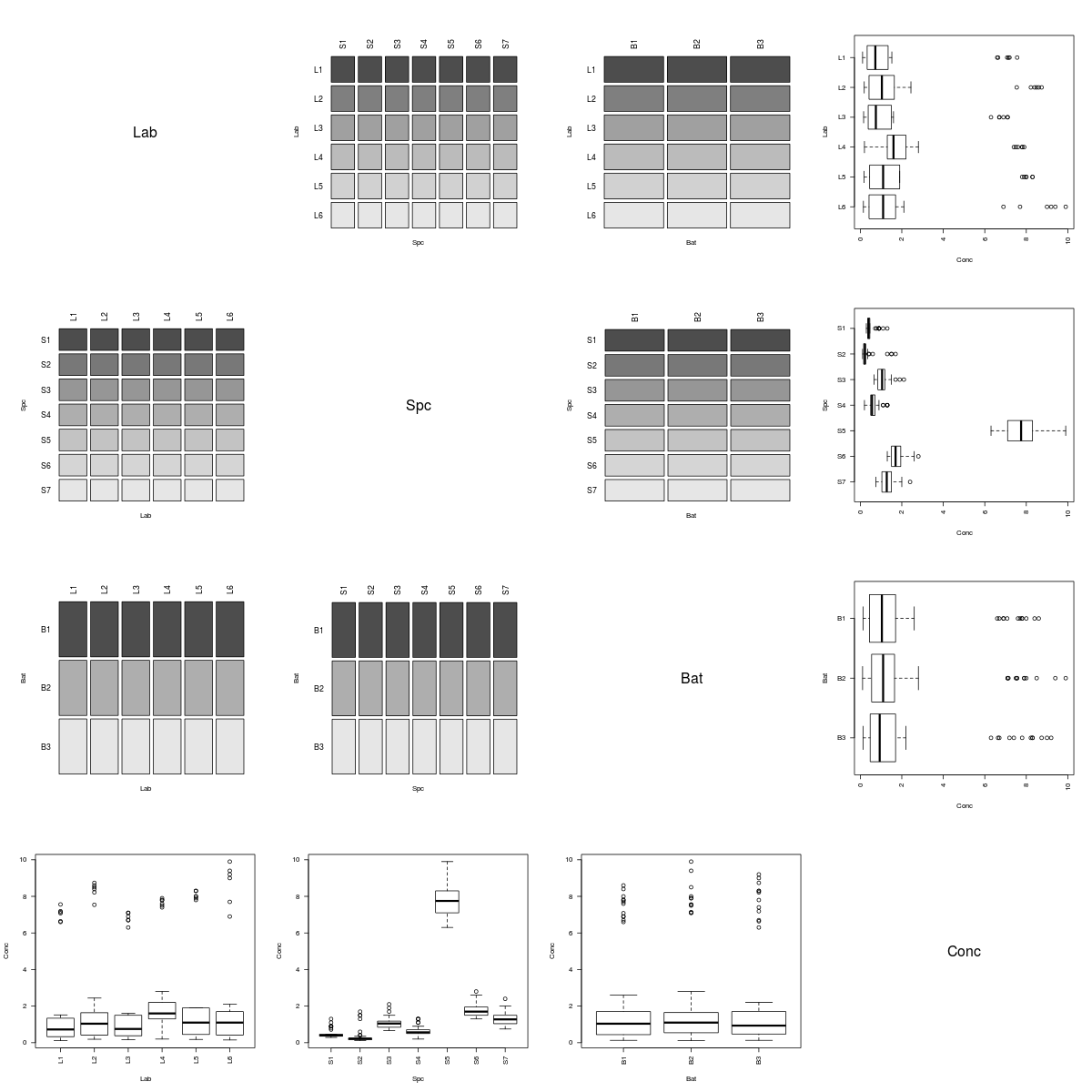
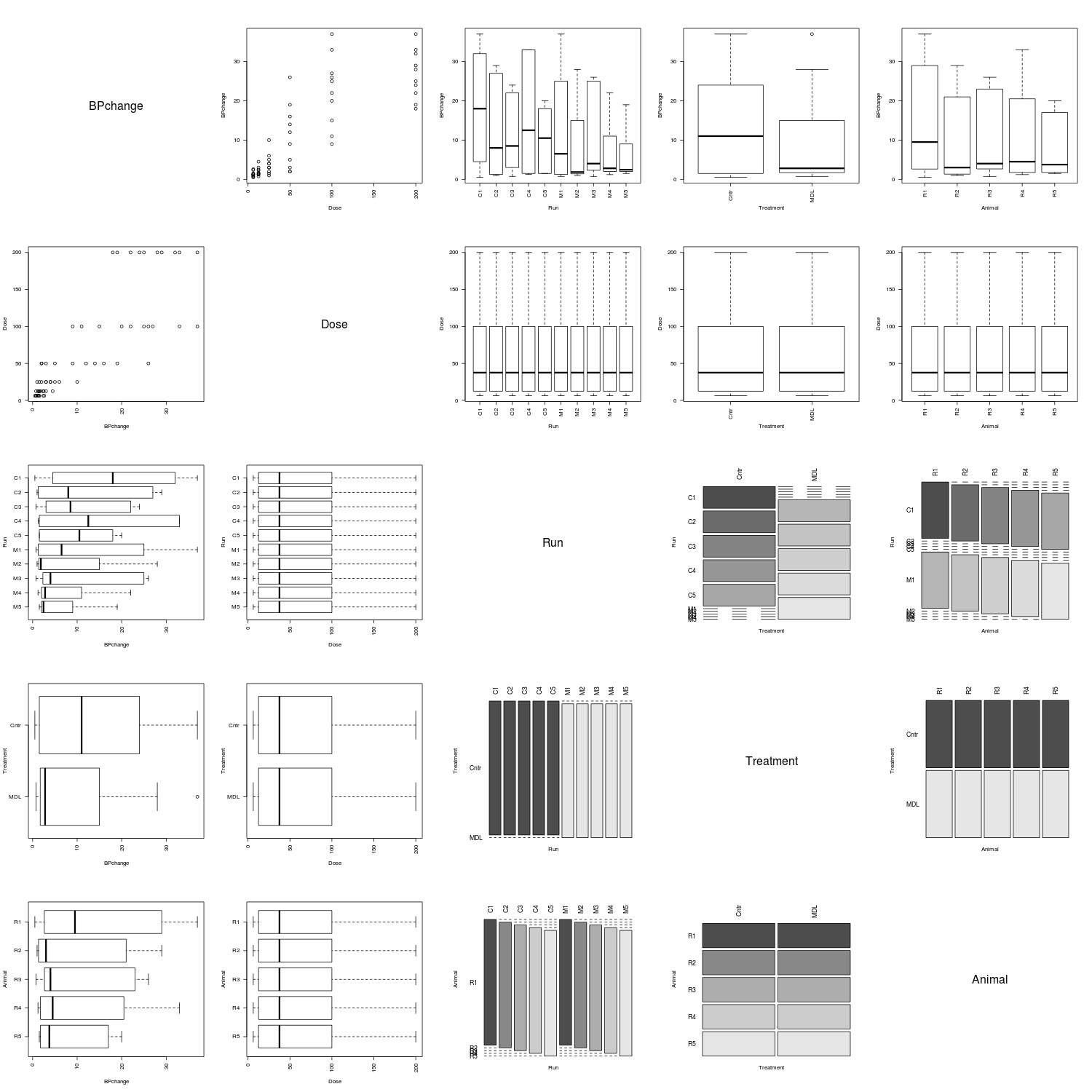
However, the Rabbit data clearly arose from a more complicated experiment.
The fields of the farms data set are all of the factor class.
{LIKE}
Great job Matt.
T
It's Emerson et al. that deserve a "well done"!
can i tell you how much us non academics like to read blog posts about aarticle behind paywalls that are $44 (us) high ?
so much fun
Here's a free, pre-print version: http://www.bricol.net/downloads/preprints,MSs,etc./11-7MSforJCGS.pdf
Nice post, looks like another very useful item from Hadley.
An alternative has been around for a while though:
library(GGally)
library(MASS)
ggpairs(Rabbit)
Yep. I missed that. Looks like it's been around since 2010.
On my very fast computer, ggpairs needs a minute for the example, your's is instantaneous; since this type of plot is explanatory often, this matters a bit.
But how did you get the plots to arrange with so little space between them? I assume there is some par(oma... stuff involved, which I was to lazy to test out on Easter Saturday morning.
Dieter
Dieter,
No fancy margin adjustments. I did have to tinker with the graphic size: ~ 3-4in per row/column seems to work well.
Matt